좌표 변환과 행렬의 곱셈

두 행렬간의 곱셈은 교환법칙이 성립하지 않음 

앞 행렬의 열의 수와 뒤 행렬의 행의 수가 같아야 곱셈 가능 

행렬의 곱셈으로 좌표 변환이 가능 

 

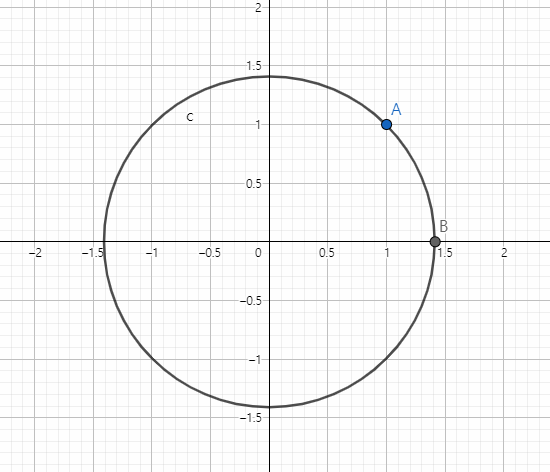
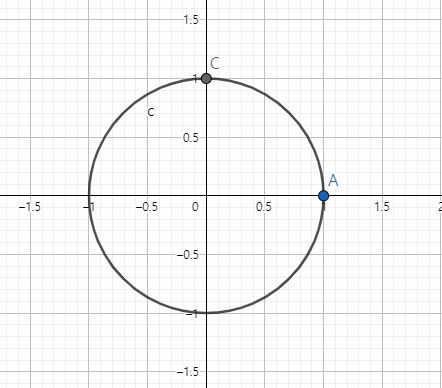
점 A에다가

을 곱하면 점 C가 된다 

 

즉, 점A에서 점C로의 좌표 변환은 다음과 같다 

 

반대로 좌표를 원상 복구 하려면 역행렬을 곱해주면 된다 

https://gammabeta.tistory.com/1116

수에 특수한 행렬을 곱하면 값이 변한다

이것을 기하학적인 의미로 좌표변환이라 한다 

 

행렬의 곱으로 물체의 좌표 이동, 크기, 회전을 계산 할수 있다 

 

 

<변환행렬> https://ko.wikipedia.org/wiki/%EB%B3%80%ED%99%98%ED%96%89%EB%A0%AC

 

---

x축 대칭이동 

---

y축 대칭이동 

---

원점 대칭이동 

---

확대 축소 행렬 

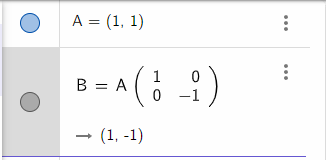
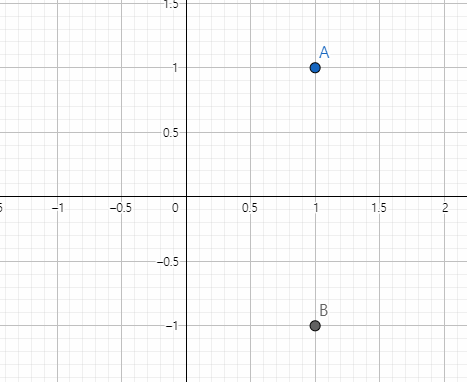
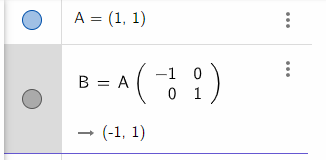
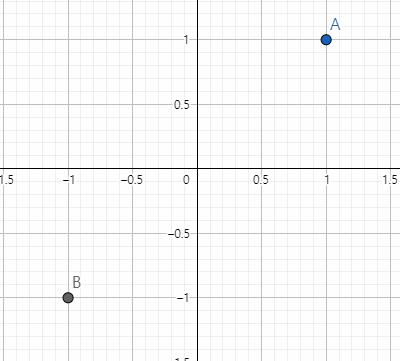
(확대 i, j > 0, 축소 i, j < 0)

 

---

 

시계방향으로 45도 회전 하는 행렬 

 c=Circle((0,0),radius)

---

반시계 방향으로 90도 회전 

---

 

 

참고

https://wiki.geogebra.org/en/Matrices

Matrices - GeoGebra 매뉴얼

https://www.geogebra.org/calculator

계산기 스위트 - GeoGebra